Ejemplo 1
Encontrar la solución del siguiente sistema de ecuaciones lineales:
a) Utilizando la Regla de Cramer.
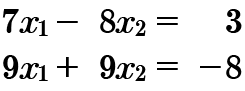
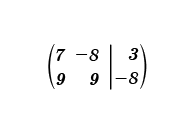
Representemos matricialmente el sistema de ecuaciones lineales a solucionar.

Construimos la matriz del determinante principal; la cual contiene solo los coeficientes de mi sistema de ecuaciones lineales, sin considerar los términos independientes.

Se realiza la multiplicación cruzada entre los elementos de la matriz; para posteriormente restar los productos.
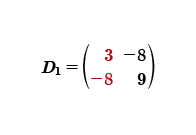
A continuación, se procederá a calcular el determinante uno, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la primera columna; la segunda columna se queda como originalmente estaba.

Se realiza la multiplicación cruzada entre los elementos de la matriz; para posteriormente restar los productos.

Se realizan las operaciones pertinentes y obtenemos el valor del determinante.
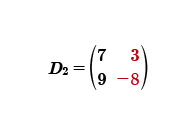
Ahora se calculará el determinante dos, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la segunda columna; la primera columna se queda como originalmente estaba.

Se realiza la multiplicación cruzada entre los elementos de la matriz; para posteriormente restar los productos.

Se realizan las operaciones pertinentes y obtenemos el valor del determinante.
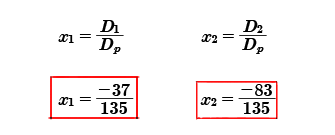
Finalmente obtendremos el valor de las incógnitas, las cuales me permiten encontrar la solución del sistema de ecuaciones lineales.

Comprobación. Para verificar que la solución del sistema es correcta, se sustituye el valor de las incógnitas X1 y X2 en cada una de las ecuaciones, con la finalidad de verificar la igualdad.