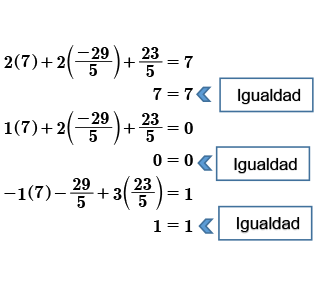
Ejemplo 3
Encontrar la solución del siguiente sistema de ecuaciones lineales:
A) Utilizando la Regla de Cramer.
B) Calcular los determinantes utilizando Propiedades.
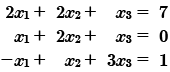
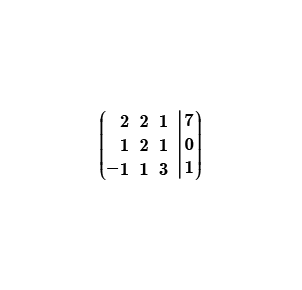
Representemos matricialmente el sistema de ecuaciones lineales a solucionar.
Resolveremos el sistema de ecuaciones lineales por la regla de Cramer; los determinantes los obtendremos utilizando propiedades.

Construimos la matriz del determinante principal; la cual contiene solo los coeficientes de mi sistema de ecuaciones lineales, sin considerar los términos independientes.
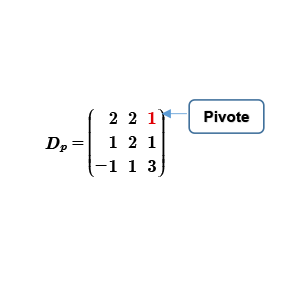
Calcularemos el determinante principal utilizando la propiedad número 1.
Vamos a generar múltiplos de un renglón a otro; es decir, hacer 1 y ceros en cualquier columna de la matriz Dp. Aprovechamos el 1 de la tercera columna para que sea el pivote y poder generar ceros debajo de él.

Multiplicamos el renglón uno R1p por el coeficiente a hacer cero, pero con signo contrario y posteriormente le sumamos el renglón donde está ubicado el coeficiente a hacer cero R1p (-1)+R2.
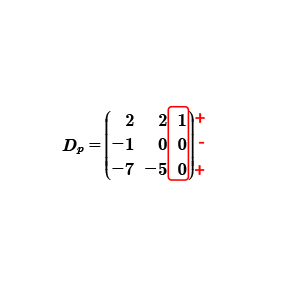
Una vez realizada la operación, procedemos a calcular el determinante de la tercera columna por formula general, no se te olvide considerar los signos que le corresponden a la columna a calcular.
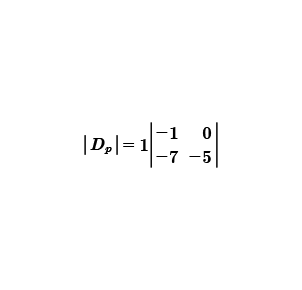
Calculamos el determinante de la matriz de 2 por 2, que resulta al eliminar el renglón uno y la columna tres.
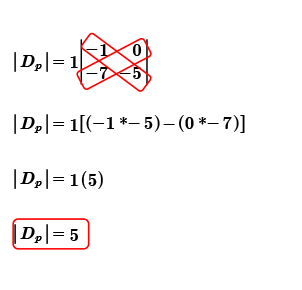
Se realiza la multiplicación cruzada entre los elementos de la matriz; para posteriormente restar los productos y con ello obtener el valor del determinante principal.
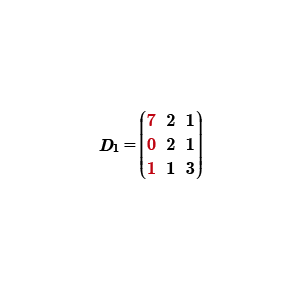
A continuación, se procederá a calcular el determinante uno, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la primera columna; la segunda y tercera columna se quedan como estaban originalmente.

Movemos el renglón 1 al 3; con la finalidad de aprovechar el 1 y 0 de la primera columna; generando una matriz triangular superior.

Consideramos al renglón uno como pivote para multiplicar por el coeficiente a hacer cero, pero con signo contrario R1p (-7) y le sumamos el renglón donde está ubicado el coeficiente a hacer cero +R3.
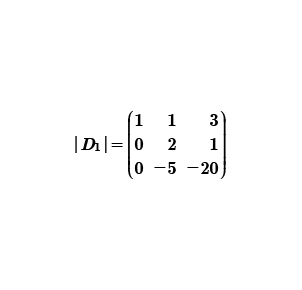
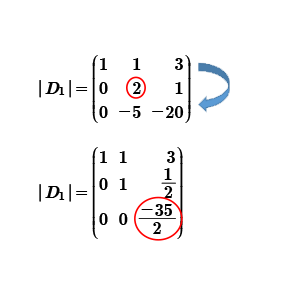
Una vez generado el cero debajo del uno, procedemos a crear el otro pivote para hacer ceros debajo de él.

El 2 es el número a hacer uno, para ello lo multiplicamos por su inverso; el inverso de 2 es ½ R2 (1/2).

Posteriormente crearemos los ceros debajo del dos; multiplicando el renglón dos pivotal por el coeficiente a hacer cero, pero con signo contrario R2p (5) y le sumamos el renglón donde está ubicado el coeficiente a hacer cero +R3.

Obteniendo la siguiente matriz triangular superior.
Para calcular el determinante se procede a multiplicar los elementos de la diagonal principal como lo indica la propiedad 4.

Por cada movimiento de renglón o columna el resultado final será multiplicado por -1, por 2 (coeficiente modificado por el valor de uno) y por -35/2, valores de la diagonal principal.

Con el cálculo de estos determinantes D1 y Dp, podremos obtener el valor de la primera incógnita.
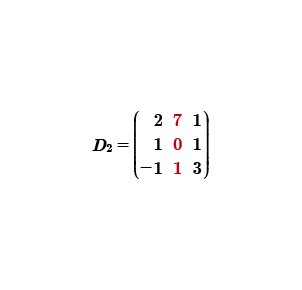
Ahora se procederá a calcular el determinante dos, está matriz esta integrada por los términos independientes, los cuales se sustituyen en la segunda columna; la primera y tercera columna se quedan como estaban originalmente.
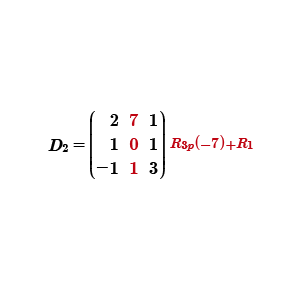
Calcularemos el determinante de la segunda columna, con la finalidad de aprovechar el renglón 3 como pivote por el 1 y el 0 de la segunda columna y solo convertir al 7 en cero, logrando reducir la matriz de 3x3 en una matriz de 2x2.

Una vez generado el cero a partir del uno, procedemos a calcular el determinante de la columna 2, utilizando fórmula general.
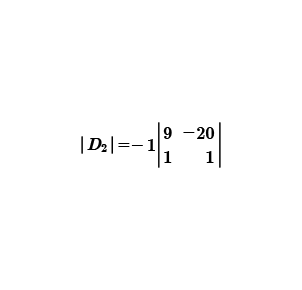
Calculamos el determinante de la matriz de 2x2, que resulta al eliminar el renglón tres de la columna dos.

Se realiza la multiplicación cruzada entre los elementos de la matriz; para posteriormente restar los productos y con ello obtener el valor del determinante dos.

Con el cálculo de estos determinantes D2 y Dp, podremos obtener el valor de la segunda incógnita.
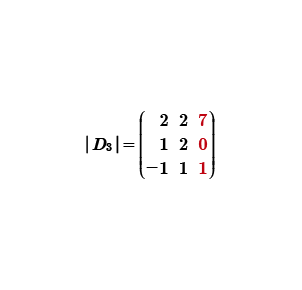
Para el cálculo del determinante de la matriz D3, la convertiremos en una matriz triangular inferior; es decir, generando ceros por arriba de la diagonal principal.
Para calcular el determinante tres, primero integramos la matriz que estará compuesta por los términos independientes, los cuales se sustituyen en la tercera columna; la primera y segunda columna se quedan como estaban originalmente.
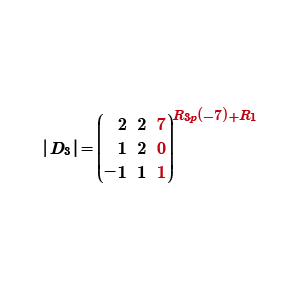
Consideramos al renglón tres como pivote para multiplicar por el coeficiente a hacer cero, pero con signo contrario R3p(-7) y le sumamos el renglón donde esta ubicado el coeficiente a hacer cero +R1.
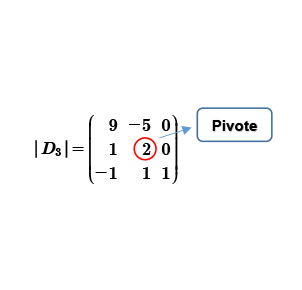
Una vez generado el cero arriba del uno, procedemos a crear el otro pivote para hacer ceros arriba de él.

El 2 es el número a hacer uno, para ello lo multiplicamos por su inverso; el inverso de 2 es 1/2 R2(1/2).

Posteriormente crearemos el cero arriba del dos; multiplicando el renglón dos pivotal por el coeficiente a hacer cero, pero con signo contrario R2p(5) y le sumamos el renglón donde esta ubicado el coeficiente a hacer cero +R1.
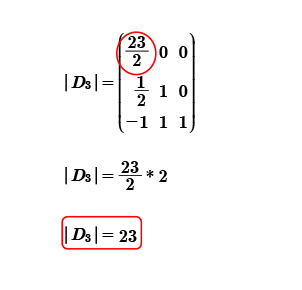
Finalmente para obtener el determinante de D3; multiplicamos los elementos de la diagonal principal.
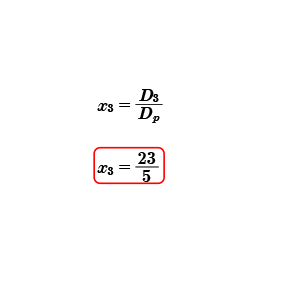
Con el cálculo de estos dos determinantes D3 y Dp, podremos obtener el valor de la tercera incógnita.