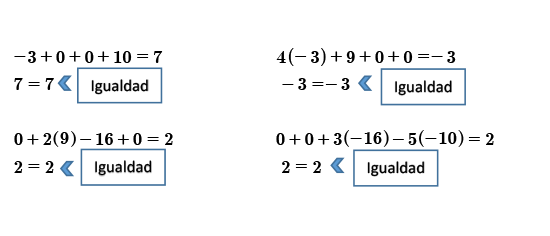
Ejemplo 4
Encontrar la solución del siguiente sistema de ecuaciones lineales:
A) Utilizando la Regla de Cramer.
B) Calcular los determinantes utilizando Propiedades y Fórmula general.
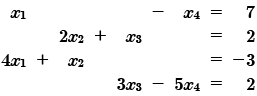
.png)
Representemos matricialmente el sistema de ecuaciones lineales a solucionar, es decir integramos los elementos o coeficientes de las ecuaciones lineales a una matriz, de esta manera podemos identificar de igual forma los ceros existentes.
.png)
Construimos la matriz del determinante principal Dp; la cual contiene solo los coeficientes de mi sistema de ecuaciones lineales, sin considerar los términos independientes.
.png)
La matriz del Dp contiene muchos unos y ceros, por lo que nos conviene transponer la matriz, con la finalidad de aprovecharlos en columna y el cálculo del determinante sea más sencillo.

Una vez transpuesta la matriz Dp; la convertiremos en una matriz triangular superior, debido a que de esta forma el cálculo del determinante es más sencillo, para ello utilizaremos el renglón 1 como pivotal R1p(1) y sumaremos el renglón 4 R4.
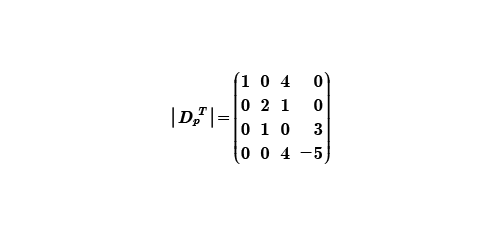
Al realizar las operaciones, anteriormente indicadas, obtenemos la siguiente matriz.

Al visualizar la matriz resultante, podemos observar que el renglón tres tiene un uno, por lo que moveremos el renglón dos al tres y así tomar al renglón dos como pivote y hacer cero al dos.
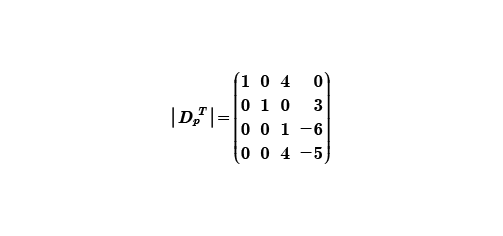
Obtenemos como resultado la siguiente matriz.

Procederemos a utilizar el uno del tercer renglón como pivote, para hacer cero el 4 del cuarto renglón R3p(-4) y sumaremos el renglón cuatro +R4.
.png)
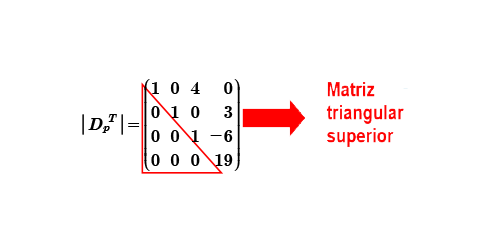
Para calcular el determinante se procede a multiplicar los elementos de la diagonal principal como lo indica la propiedad 4 y por cada movimiento de renglón o columna el resultado final será multiplicado por -1, por 19 valor de la diagonal principal.
.png)
A continuación, se procederá a calcular el determinante uno, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la primera columna; la segunda, tercera y cuarta columna se quedan como estaban originalmente.
.png)
Continuaremos utilizando las propiedades; por lo que la matriz D1, la convertiremos en una matriz triangular inferior, para ello, realizaremos un movimiento del renglón 1 al renglón 4 y viceversa; con la finalidad de aprovechar el uno del primer renglón y los ceros de la cuarta columna.
.png)
Multiplicaremos el renglón 1 por -1, para hacer pivote al renglón 1, al final del cálculo del determinante se deberá multiplicar por -1, debido a que se alteró la matriz al convertir en uno positivo.
.png)
Una vez realizado el cambio de renglón y haber convertido al uno en positivo, se procederá a hacer cero al -5 R4p(5)+R1.
.png)
Obteniendo la siguiente matriz, en la cual se procederá a hacer otro movimiento de renglón, del renglón 2 al 3 y viceversa, para aprovechar el uno y ubicarlo en la diagonal principal.
.png)
Hacemos cero al tres del renglón uno con el pivote del renglón tres, quedando la siguiente matriz resultante.
.png)
Posteriormente convertiremos a -6 en cero, con el renglón pivotal dos.
.png)
Para calcular el determinante se procede a multiplicar los elementos de la diagonal principal como lo indica la propiedad 4 y por cada movimiento de renglón o columna que se haya tenido, el resultado final deberá ser multiplicado por -1 y por -57 valor de la diagonal principal.
.png)
Con el cálculo de estos dos determinantes D1 y Dp, podremos obtener el valor de la primera incógnita.
.png)
Ahora se procederá a calcular el determinante dos, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la segunda columna; la primera, tercera y cuarta columna se quedan como estaban originalmente.
.png)
Continuaremos utilizando las propiedades; pero ahora nos auxiliaremos con la fórmula general, para ello, primero generamos ceros debajo del uno de la primera columna.
.png)
Obteniendo de esta forma la siguiente matriz.
.png)
Procederemos a calcular el determinante de la columna uno, debido que al generar unos y ceros, la matriz reduce su grado, es decir de una matriz de 4x4, se convierte a una matriz de 3x3, de la cual el cálculo será por fórmula general.
.png)
Calculando el determinante de la columna uno, por fórmula general, obtendremos la siguiente matriz de 3x3.
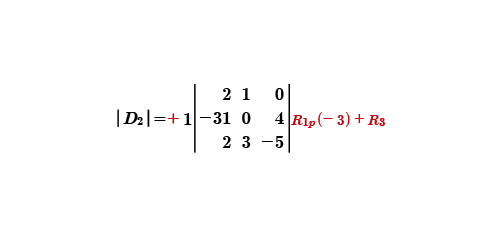
Para resolver la matriz de 3x3, utilizamos el renglón uno como pivote y hacemos cero al tres R1p(-3)+R3 de la segunda columna.
.png)
Una vez generado el cero, se calcula el determinante de la segunda columna, obteniendo así una matriz de 2x2.
.png)
Resolviendo la matriz de 2x2, obtenemos el valor de |D2|.
.png)
Con el cálculo de estos dos determinantes D2 y Dp, podremos obtener el valor de la segunda incógnita.
.png)
Podemos utilizar el mismo procedimiento que en el cálculo del determinante |D2|, pero ahora para calcular |D3| matriz integrada por los términos independientes, los cuales se sustituyen en la tercera columna; la primera, segunda y cuarta columna se quedan como estaban originalmente.
.png)
Continuaremos utilizando las propiedades; nuevamente nos auxiliaremos con la fórmula general, para ello, primero generamos ceros debajo del uno de la primera columna.
.png)
Obteniendo de esta forma la siguiente matriz:
.png)
Procederemos a calcular el determinante de la columna uno, debido que al generar unos y ceros, la matriz reduce su grado, es decir de una matriz de 4x4, se convierte a una matriz de 3x3, de la cual el cálculo será por fórmula general.
.png)
Calculando el determinante de la columna uno, por fórmula general, obtendremos la siguiente matriz de 3x3.
.png)
Para resolver la matriz de 3x3, utilizamos el renglón dos como pivote y hacemos cero al dos R2p(-2)+R1 de la primera columna.
.png)
Quedando la matriz de la siguiente manera:
.png)
Una vez generado el cero, se calcula el determinante de la primera columna, por fórmula general, obteniendo así una matriz de 2x2.
.png)
Resolviendo la matriz de 2x2, obtenemos el valor de |D3|.
.png)
Con el cálculo de estos dos determinantes D3 y Dp, podremos obtener el valor de la tercera incógnita.
.png)
Continuaremos utilizando propiedades con fórmula general, pero ahora para calcular |D4|, la matriz estará integrada por los términos independientes, los cuales se sustituyen en la cuarta columna; la primera, segunda y tercera columna se quedan como estaban originalmente.
.png)
Continuaremos utilizando las propiedades; nuevamente nos auxiliaremos con la fórmula general, para ello, primero generamos ceros debajo del uno de la tercera columna, considerando el renglón dos pivotal y convirtiendo a cero a tres R2p(-3)+R4.
.png)
Obteniendo de esta forma la siguiente matriz:
.png)
Procederemos a calcular el determinante de la columna tres, debido que al generar unos y ceros, la matriz reduce su grado, es decir de una matriz de 4x4, se convierte a una matriz de 3x3, de la cual el cálculo será por fórmula general.
.png)
Calculando el determinante de la columna tres, por fórmula general, obtendremos la siguiente matriz de 3x3.
.png)
Para resolver la matriz de 3x3, utilizamos el renglón uno como pivote y hacemos cero al cuatro R1p(-4)+R2 de la primera columna.
.png)
Quedando la matriz de la siguiente manera:
.png)
Una vez generado el cero, se calcula el determinante de la primera columna, por fórmula general, obteniendo así una matriz de 2x2.
.png)
Con el cálculo de estos dos determinantes D4 y Dp, podremos obtener el valor de la cuarta incógnita.
.png)