Ejemplo 5
Encontrar la solución del siguiente sistema de ecuaciones lineales:
A) Utilizando la Regla de Cramer.
B) Calcular los determinantes utilizando el método de Sarrus.
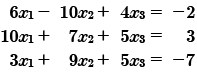
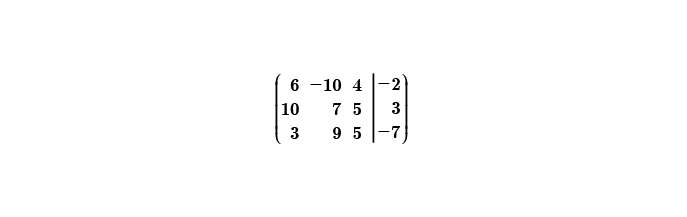
Representemos matricialmente el sistema de ecuaciones lineales a solucionar, es decir integramos los elementos o coeficientes de las ecuaciones lineales a una matriz. Daremos solución a este sistema de ecuaciones lineales por regla de Cramer; los determinantes los obtendremos por Sarrus.
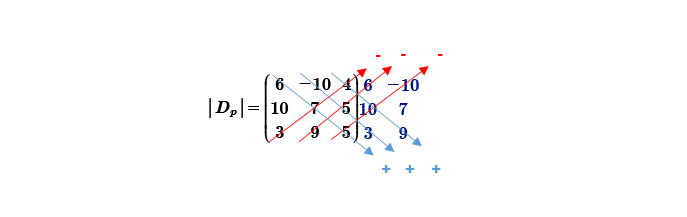
Para utilizar Sarrus; aumentamos las dos primeras columnas de la matriz; identificamos la diagonal principal y las 2 diagonales subsecuentes; efectuamos una suma con los productos; identificamos la diagonal invertida y las 2 subsecuentes; efectuamos una resta con los productos.
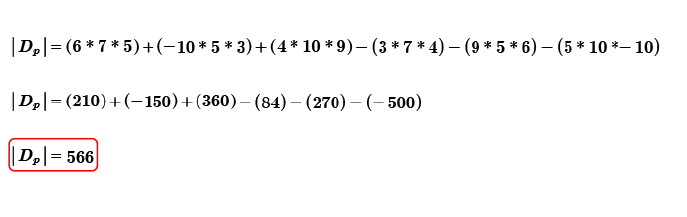
Procedemos a realizar las respectivas operaciones.
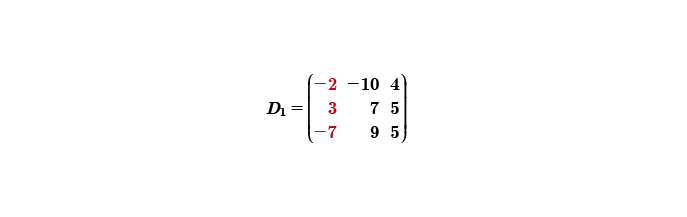
A continuación, se procederá a calcular el determinante uno, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la primera columna; la segunda y tercera columna se quedan como estaban originalmente.

Aumentamos las dos primeras columnas de la matriz; identificamos la diagonal principal y las 2 diagonales subsecuentes; efectuamos una suma con los productos; identificamos la diagonal invertida y las 2 subsecuentes; efectuamos una resta con los productos.

Con el cálculo de estos dos determinantes D1 y Dp, podremos obtener el valor de la primera incógnita.
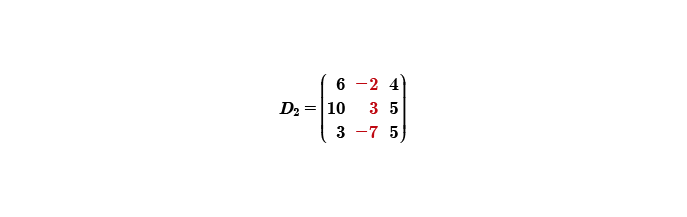
Ahora se procederá a calcular el determinante dos, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la segunda columna; la primera y tercera columna se quedan como estaban originalmente.

Para obtener |D2|, nuevamente agregamos las 2 primeras columnas, identificamos diagonal principal y las 2 subsecuentes, multiplicamos los productos y sumamos o restamos.

Con el cálculo de estos dos determinantes D2 y Dp, podremos obtener el valor de la segunda incógnita.
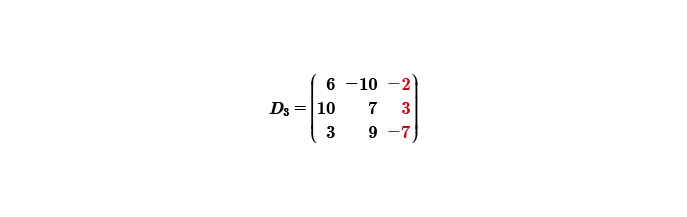
Calcular el determinante tres, esta matriz está integrada por los términos independientes, los cuales se sustituyen en la tercera columna; la primera y segunda columna se quedan como estaban originalmente.

Para obtener |D3|, nuevamente agregamos las 2 primeras columnas, identificamos diagonal principal y las 2 subsecuentes, multiplicamos los productos y sumamos o restamos.

Con el cálculo de estos dos determinantes D3 y Dp, podremos obtener el valor de la tercera incógnita.
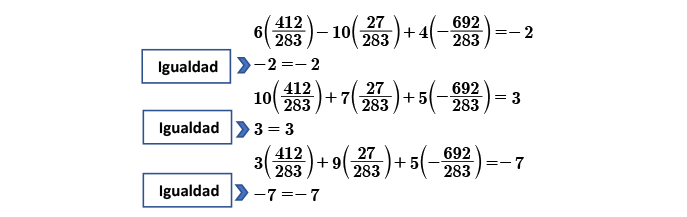
Comprobación. Con el valor de cada una de las incógnitas, podremos comprobar que el resultado obtenido es correcto, para ello sustituimos estos valores en las tres ecuaciones originales, para verificar que nos resulten las igualdades.