Un cofactor es igual: A_ij = -1^(i+j) | M_ij |

Donde: i = renglón ; j = columna

Si:

i + j = par, corresponde un signo +

i + j = impar, corresponde un signo -

Corresponde: | M_ij | = Matriz resultante al eliminar el renglón y columna seleccionado

Ejemplo de una matriz de 3 x 3

Comenzamos por definir un determinante de 3 x 3.

Sea A una matriz cuadrada de 3 por 3; tres renglones y tres columnas

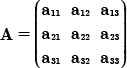
Primero se analiza en la matriz que renglón o columna es conveniente elegir para calcular el determinante; con la finalidad de generar menos procedimiento, cualquier renglón o columna crea el mismo resultado.

También el método de cofactores es denominado menores cofactores

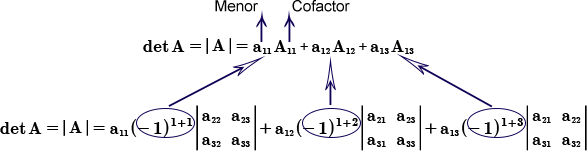
Recuerda que:

Un cofactor es igual: A_ij = -1^(i+j) | M_ij |

Definir el signo que genera el cofactor, quedando la siguiente expresión:

Recuerda que:

i + j = par, corresponde un signo +

i + j = impar, corresponde un signo -