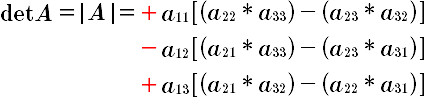Algoritmo del cálculo del determinante por fórmula general
Para calcular el determinante de una matriz de n x n (matriz cuadrada) por fórmula general, se usa lo que se sabe sobre un determinante de 2 x 2, para definir un determinante de 3 x 3, que a su vez se usa para definir un determinante de 4 x 4, y así sucesivamente.
Comenzamos por definir un determinante de 3x3.
Sea A una matriz cuadrada de tres por tres; tres renglones y tres columnas:

Primero se analiza en la matriz que renglón o columna es conveniente elegir para calcular el determinante; con la finalidad de generar menos procedimiento, cualquier renglón o columna crea el mismo resultado.
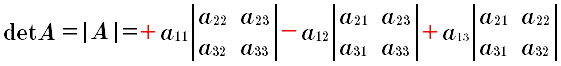
Para obtener las matrices del renglón o columna elegido; solo se elimina el renglón y columna que ocupa el coeficiente, ejemplo: