Visualizar en la matriz que renglón o columna es conveniente elegir para calcular el determinante; cualquier renglón o columna crea el mismo resultado. Lo más conveniente es obtener el determinante de la columna 3 o el renglón 4; esto debido a la existencia del cero, lo que reduce un cálculo.

En este caso se calcula el determinante con la columna 3, colocando los signos que le corresponde.

Se desintegra la matriz; primeramente, se obtendrán cinco matrices de 4x4, posteriormente veinte matrices de 3x3 y finalmente 60 matrices de 2x2.
Los signos que le corresponden a la columna, van multiplicados por los signos que tienen los coeficientes, como hay un cero en la columna, solo se generan cuatro matrices de 4x4.

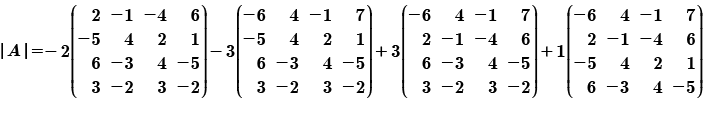
Resolver cada una de las cuatro matrices de orden 4x4; por conveniencia se asignan algunos términos a cada una de estas matrices para poder diferenciar los cálculos.

Repetir el algoritmo, seleccionar un renglón o columna de cada matriz para calcular el determinante, colocar los signos que corresponden a cada renglón o columna.
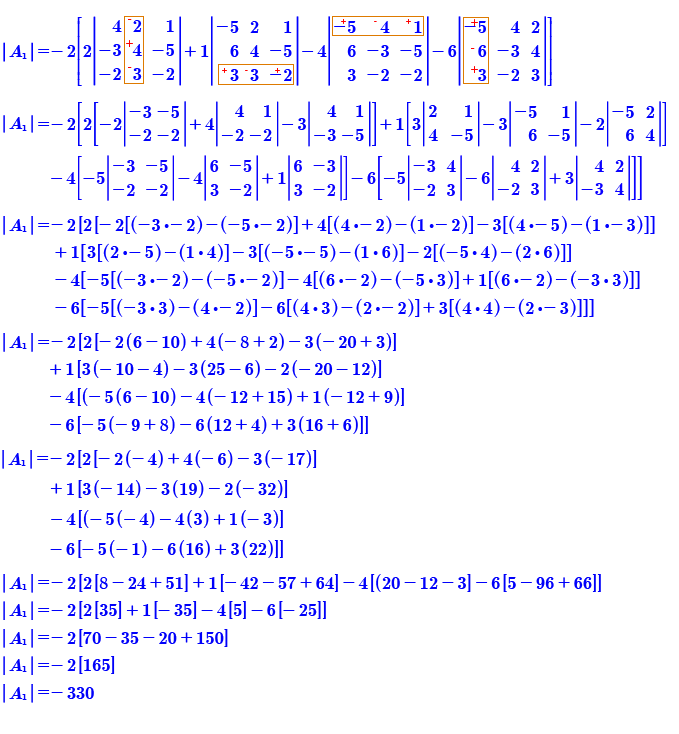
Cada matriz de 4x4 genera 4 matrices de 3x3, nuevamente colocar los signos que correspondan al renglón o columna seleccionada. Se inicia el cálculo del determinante de la matriz |A₁|.

Cada una de las matrices de 3x3, genera 3 matrices de 2x2; para calcular el determinante de una matriz de 2 x 2 se realiza una multiplicación cruzada y se restan los productos.

|A|=|A₁|+|A₂|+|A₃|+|A₄|
|A|=(-330)+(-300)+(-489)+(-159)
|A|=-1278