Se muestra un ejemplo para el cálculo del determinante de una matriz de 5x5, utilizando cofactores.

Para esta matriz, lo más conveniente es obtener el determinante de la columna 3 o el renglón 4; esto debido a la existencia del cero, lo que reduce un cálculo.

El cálculo del determinante del cuarto renglón, nos arroja 4 matrices de 4 por 4, la matriz del coeficiente cero a₄₃A₄₃ ya no se calcula.

Al desarrollar la expresión, nos queda:
A_T=a₄₁A₄₁+a₄₂A₄₂+a₄₃A₄₃+a₄₄A₄₄+a₄₅A₄₅

Resolver cada una de las cuatro matrices de orden 4 por 4; se asignan algunos "Términos" a cada una de estas matrices para poder diferenciar los cálculos. Este cálculo arroja veinte matrices de 3 por 3 y finalmente 60 matrices de 2 por 2.

Repetir el algoritmo, seleccionar un renglón o columna de cada matriz de 4 por 4 para calcular el determinante.

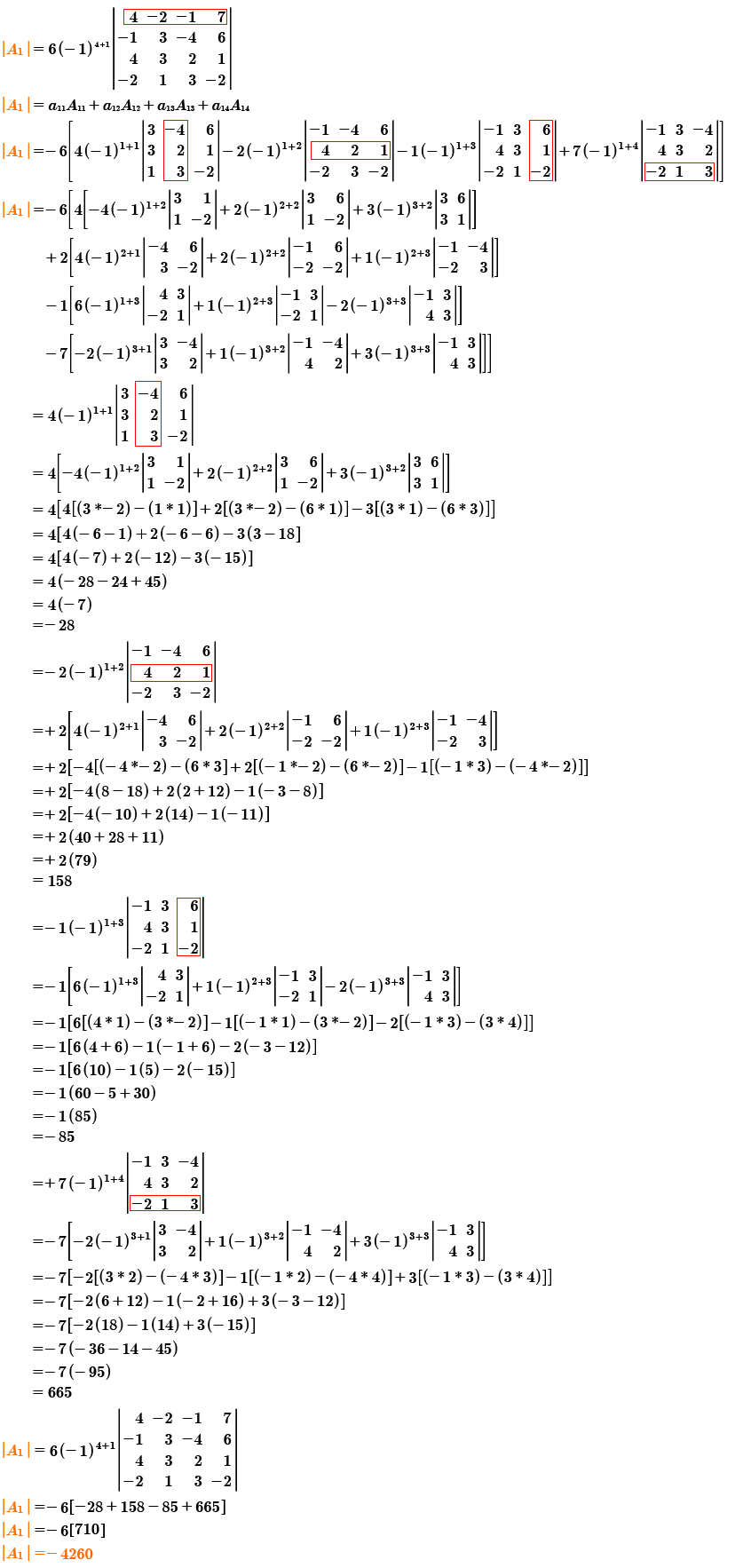
Cada matriz de 4 por 4 genera 4 matrices de 3 por 3. Se inicia el cálculo del determinante de la matriz |A₁|

|A_T|=|A₁|+|A₂|+|A₃|+|A₄|
|A_T|=(-4260)+(2982)+(0)+(0)
|A_T|=-1278