Anteriormente estudiamos como se factoriza una diferencia de cuadrados y vimos las condiciones que debe tener una expresión algebraica para ser un cuadrado perfecto, en este caso haremos algo similar, para comenzar damos una lista de las potencias al cubo de los primeros treinta números naturales.

Cuando sacamos la raíz cúbica de cado uno de los números anteriores da como resultado un número entero, en cuyo caso decimos que es un número cúbico perfecto, no obstante, no todos los números tienen esta característica, por ejemplo: el número 10 no es cúbico perfecto, pues su raíz cúbica no resulta ser un número entero. Así mismo, cuando calculamos la raíz de una incógnita elevada a una potencia, diremos que es un cúbico perfecto si al sacar su raíz resulta que el exponente es un número entero.

Por ejemplo, 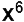es cúbico perfecto, pues 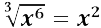, no obstante 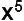no lo es, dado que al obtener su raíz cúbica resulta que el exponente es 5/3, así los únicos exponentes que admiten que la incógnita sea cúbico perfecto son los exponentes múltiplos de 3.

Algunos ejemplos de monomios que son cúbicos perfectos son los siguientes.

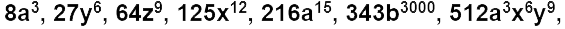etc.

Ahora bien cuando hablamos de una diferencia o suma de dos cúbicos, nos referimos a la resta o suma de dos monomios de la forma anterior. Cabe mencionar que podemos obtener una diferencia de cúbicos de cualquier expresión algebraica. Nosotros solo obtendremos la factorización de dos cúbicos perfectos. En el siguiente video se muestra la factorización de dichas estructuras algebraicas.

Ejemplo:

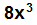es un cubo perfecto, dado que 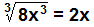, 2 es un entero y el exponente de x es 1 que también es entero, no obstante 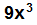no es un cuadrado perfecto pues 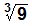no es un entero.

Ejercicio:

¿Verdadero o Falso? 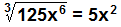? Ver respuesta Verdadero