La factorización por término común está ligada a una de las propiedades de los números reales, llamada propiedad distributiva, esta propiedad dice que para cuales quiera a, b y c en los números reales, se cumple que ac + bc = c(a + b)
En este caso decimos que la factorización de ac + bc es c(a + b)
Ejemplo: Considere la suma 5∙8 + 5∙9.
Dado que el número 5 aparece en ambos sumandos, la suma se puede reescribir como un producto.
5∙8 + 5∙9 = 5(8+9)
Del lado izquierdo de la igualdad se tiene 5∙8 + 5∙9 = 40 + 45 = 85, mientras que por el lado derecho se tiene 5(8+9)=5(17)=85, llegando al mismo resultado.
De manera natural podemos extender esta idea para una cantidad más grande de números reales.
Por ejemplo, si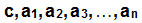 
representan algún número real. Entonces se cumple lo siguiente: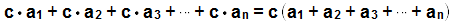 
Ejemplo:
3∙6 + 3∙2 + 3∙4 + 3∙3 + 3∙5 = 3∙(6+2+4+3+5)
18+6+12+9+15
3(20)
60
60
Ejercicio:
Factoriza la siguiente suma:
7∙8 + 7∙3 = ? Ver respuesta 7(8+3)
La idea de factorizar sumas donde únicamente se usan números, se puede extender aún más cuando se trabaja con polinomios de grado mayor o igual a uno.
Diremos que una factorización por término común es aquella en la cual podemos representar una suma de términos como un producto, donde uno de los factores contiene a los elementos que cada sumando tiene en común.