Hace un par de siglos, matemáticos reconocidos intentaron encontrar fórmulas para factorizar a un polinomio de grado n, con n un número natural, sin embargo la búsqueda de estas fórmulas no tuvieron éxito, ahora sabemos que en general no se puede factorizar a cualquier polinomio de grado n, afortunadamente para el caso n igual a 2, es decir para polinomios de la forma 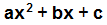, existen diversos métodos.

Uno de ellos se determina como sigue: 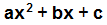como producto de dos binomios, para eso deben de existir valores: d, e, f y g tales que:

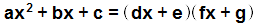
Como 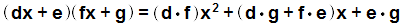, (desarrollamos el producto)

Entonces la igualdad entre el polinomio original y el que resulta de desarrollar el producto de binomios se cumple solamente si pasa lo siguiente:

• a= d•f
• b= (d•g + f•e)
• c= e•g

Con esto podemos plantear una regla:

Dado un polinomio de la forma 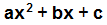, debemos encontrar valores d, e, f y g que hagan que se cumpla lo anterior, es decir.

• a= d•f
• b= (d•g + f•e)
• c= e•g

Así, si logramos resolver las 3 ecuaciones anteriores obtendremos la facorización: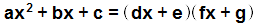

Este proceso lo representamos de manera general para encontrar la regla anterior.

A continuación realizaremos un ejemplo, haciendo uso de dicha regla.

Ejemplo: Factoriza a 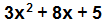llenando los espacios:

Queremos que:

• 3= d•f
• 8= d•g + f•g
• 5 = e•g

Si d = 3 y g = 1, entonces: 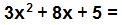? Ver respuesta (3x + 5) (1x + 1)

Además de este método, existen diversos procesos algorítmicos que nos llevan a encontrar una factorización de manera más sistemática, como el que se muestra en el siguiente video.