Como ya hemos visto, el problema de factorizar polinomios cuadráticos se puede abordar con distintos métodos, pero quizás uno de los más sencillos es descubrir los factores con la regla planteada en el apartado Introductorio, donde únicamente se hace uso de multiplicaciones y sumas de los factores de “a” y “c” (los factores del coeficiente del término cuadrático y los factores del término constante).

En particular, será más sencillo encontrar dichos factores cuando el coeficiente principal es un número primo, (un número natural se dice primo si es distinto de 1 y solo es dividido por 1 y por él mismo, por ejemplo: 2, 3, 5 y 7) veamos el siguiente ejemplo:

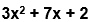
Como 3 y 2 son números primos sus únicos factores serán 1 y 3 para el coeficiente principal y únicamente 2 y 1 para el término constante, entonces solo debemos aplicar la regla dada en el apartado introductorio.

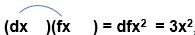, podemos poner d=3 y f=1

, entonces alguno de e o g debe ser 2 y el otro debe de ser 1, eso lo determinaremos con el último desarrollo.

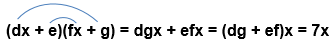
Ahora, solo basta asignar bien a los factores encontrados para que sumen 7.

En este caso será e=1 y g=2 (pues los términos d y f ya los habíamos fijado como: d=3 y f=1, obteniendo dg + ef = 3•2 + 1•1= 6 + 1 =7).

Así, se tiene que: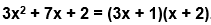

Si el alumno es más metódico puede usar el algoritmo dado en el video y si le gusta más hacer cálculos, puede usar el proceso usado en el apartado introductorio.