Tema: 1
Matrices

1.4 Tipos de matrices
Algunas matrices destacables son:
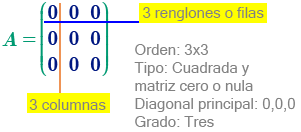
Matriz nula, es aquella cuyos elementos son todos cero.

Matriz fila, la cual cuenta con una sola fila.
Matriz columna, la cual cuenta con una sola columna.
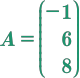
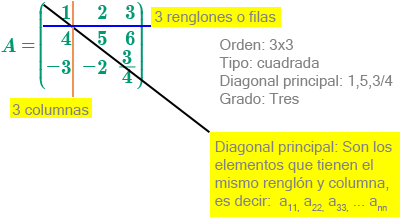
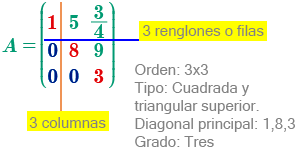
Matriz cuadrada, es aquella que tiene el mismo número de filas que de columnas, es decir, de dimensión \(n * n\) por ejemplo:
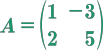
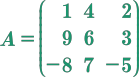
Las matrices cuadradas son las únicas que poseen grado, el cual es igual al número de orden.
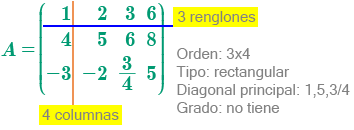
Matriz rectangular, es aquella matriz donde m es diferente de n, es decir, desigual número de renglones y de columnas, por ejemplo:

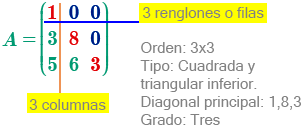
Matriz triangular, es una particularidad de la matriz cuadrada, cuando los elementos por encima o por debajo de la diagonal principal están conformados por \(0\) dependiendo donde se encuentren, es el nombre con que se designa.
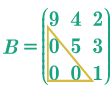
Matriz triangular superior.

Matriz triangular inferior
Matriz diagonal, es la matriz cuadrada cuyos elementos que se encuentran sobre y por debajo de la diagonal principal son \(0\).
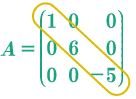
Diagonal principal.
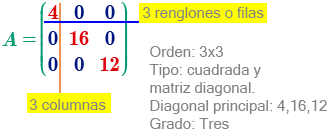
Matriz escalar, es toda matriz diagonal en la cual los elementos de la diagonal principal son iguales.
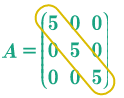
Diagonal principal.
Matriz identidad, es la matriz diagonal en la que todos los elementos de la diagonal principal son números 1. Se representa con la letra \(I\).
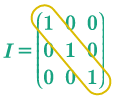
Diagonal principal.

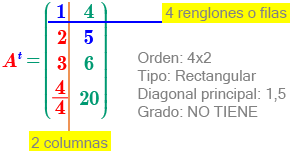
Traspuesta de una matriz, se representa de la siguiente forma \(A^T\) la característica es que cambian de posición los elementos de la fila y columna.
\(A = (a\)\(ij\)\()\) de orden \(m * n\) si se modifica a una matriz traspuesta quedaría \(A^T = (a\)\(ij\)\()\) y se modifica al orden \(n * m\)

Se cambian filas a columnas y las columnas a filas quedando de la siguiente forma:
Matriz simétrica. Una matriz es simétrica cuando es igual a su traspuesta. \(A = A^T\)
Sólo se aplica a una matriz cuadrada.
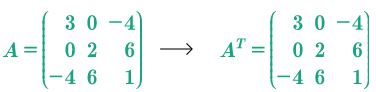
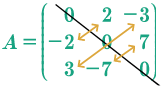
Modo práctico. Se puede visualizar si una matriz es simétrica si los elementos que se reflejan respecto a la línea que pasa por la diagonal principal son iguales.

Matriz antisimétrica. Una matriz es antisimétrica cuando esta resulta igual a menos su traspuesta. \(A = -A^T\)

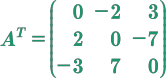
Se multiplica la traspuesta por\(-1\)

El resultado es una matriz igual a la primera.
Modo práctico. La diagonal debe contener elementos, \(0\) y los elementos que se reflejan deben ser opuestos.