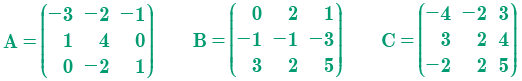Tema: 1
Matrices

1.8 Multiplicación de matrices
CARACTERÍSTICAS PRINCIPALES:
- No existe conmutatividad en la multiplicación de matrices, es decir, AB BA
- Si existe distributividad, es decir, A(B+C) = AB + AC
- Si existe asociatividad, es decir, (AB)C = A(BC)
- Para que se dé la multiplicación con matrices, no importa su orden, siempre y cuando las columnas de la primera matriz sean iguales con los renglones de la segunda matriz.
- El orden del producto de la matriz, nos lo indica, el número de los renglones de la primera matriz y el número de las columnas de la segunda matriz.
Ejemplo:
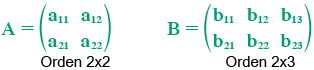

Una vez satisfecha la condición, se procede a multiplicar cada uno de los renglones de la primera matriz por cada una de las columnas de la segunda matriz, efectuando una suma con los productos.

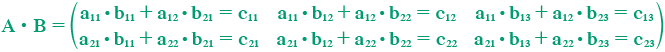
Ejemplo 1:
Dadas las siguientes matrices A y B, calcular: A B



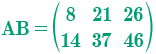
Ejemplo 2:
Dadas las siguientes matrices A y B, calcular: A B

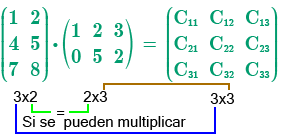

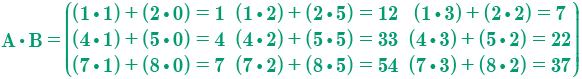

Ejemplo 3:
Dadas las siguientes matrices A y B, calcular: A B

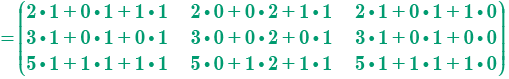
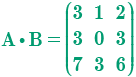
Ejemplo 4:
Dadas las siguientes matrices A y B, calcular: A B


Ejemplo 5:
Dadas las siguientes matrices A, B y C calcular: A B, B C, C B A